Find the Rank and Nullity of the Matrix

We have AB 0 Then we get b1 2b2 0 b3 0 The null vector we can get is The number of parameter in the general solution is the dimension of the null space which is. For the given matrix A find a The rank of the matrix A b a basis for the row space c a basis for the column space.

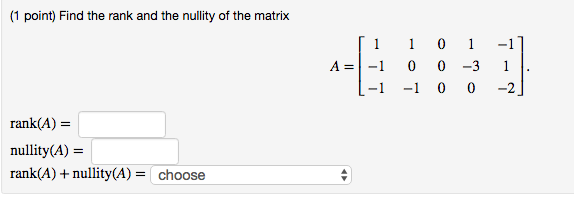
Solved Find The Rank And The Nullity Of The Matrix A Chegg Com

Let A be an m by n matrix with rank r and nullity ℓ.

. That is rank A nullity A the number of columns of A. Rank is 2 and hence Nullity is 1. Mat 10 20 10 20 40 20 30 50 0 Output.

A set of n-elements of which are linearly independent is. Therefore the Nullity of the matrix will be the number of columns in the matrix-Rank which will be 1 for the above matrix. 100 11 ratings The row reduced form of.

In other words rankAnullityA number of columns of A. Theorem 3 The rank of a matrix A plus the nullity of A. Rank and Nullity of a Matrix Nullity of Transpose Let A be an m n matrix.

Row space of a matrix. The nullspace of A is denoted by N A. By the Rank-Nullity Theorem nullityA n r.

Solve it with our. Next take the matrix values from the input and store. C o l u m n s r a n k n u l l i t y text columnstext ranktext nullity columns rank nullity.

2 To find nullity of the matrix simply subtract the rank of our Matrix from the total number of columns. Thus from Theorem 4610 if x1x2xnr is any set of nr linearly independent solutions. The Rank Plus Nullity Theorem.

Ist and IInd rows are linearly. This can be generalized further to linear maps. For part b.

A N A N A T A. 3411 Theorem Rank Nullity. Variables in a system can be separated in two categories.

We have number of leading variables. What we can say then is that the sum of the nullity and the rank of a matrix will be equal to the total number of columns in the matrix. The dimension of the nullspace of A is called the nullity of A.

1 To find the rank simply put the Matrix in REF or RREF. Show N A N A T A Consider any x N A. Rank rank 3 nullity nullity 1 AA AA but RA RA because of the matrix multiplications on the left.

For part b use the rank-nullity theorem and the result from a. If there is a matrix M M with x x rows and y y columns over a field then text rank M text nullity M y. The sum of the nullity and the rank 2 3 is equal to the number of columns of the matrix.

The rank of a matrix rows columns is the maximum number of linearly independent rows columns of this matrix. The rank of the matrix A which is the number of non-zero rows in its echelon form are 2. Corollary The rank of a matrix is equal to the number of nonzero rows in its row echelon form.

B rank A rank A T A Hint. The rank-nullity theorem is defined as Nullity X Rank X the total number of attributes of X that are the total number of columns in X How to Find Null Space of a Matrix. B rank A rank A T A.

This is the best answer based on feedback and ratings. See the answer See the answer done loading. The connection between the rank and nullity of a matrix illustrated in the preceding example actually holds for any matrix.

Keith Wojciechowski 139K subscribers Subscribe Given a matrix use elementary row operations to reduced the matrix to rref then determine the rank and nullity using the theorem rank. For the given matrix A find a The rank of the matrix A b a basis for the row space c a basis for the column space. The rank nullity theorem helps to link the nullity of the data matrix with the ranking and number of attributes in the data.

Let A be a m n matrix with rank A r. Show transcribed image text. Rank of a matrix.

The rank-nullity theorem says that for a m n matrix rank of A nullity of A n. Multiplying it by A T from the left we obtain. This problem has been solved.

In this video I will walk you through an example where we find the null space and the nullity of a matrix. Hence rank A nullity A n. The leading variables the ones corresponding to the leading 10s and the free variables the ones to which we usually assign a parameter.

You can use the rank nullity theorem to find the nullity. The rank of a matrix A is the rank of its rows or columns. A N A N A T A.

The rank-nullity theorem states that the rank and the nullity the dimension of the kernel sum to the number of columns in a given matrix. 0 0 0 0 0 05 05 0 0 05 05 0 R R E F 0 0 0 0 0 05 05 0 0 0 0 0 Seeing that we only have one leading variable we can now say that the rank is 1. Use The Rank Plus Nullity Theorem it says Nullity rank number of columns n Therefore you will be able to calculate nullity as Nullity no.

Then we have A x 0. The null space is expressed as the span of a basis. Previous question Next question.

Then nullity A r. 49 The Rank-Nullity Theorem 309 Proof Note that part 1 is a restatement of previous results or can be quickly deduced from the Rank-Nullity Theorem. 1 point Find the rank and the nullity of the matrix -2 -2 -1 -3 À is és A -1 -1 1 4 0 -1 -1 -4 0 rankA nullityA rankA nullityA choose.

First Take the number of rows and columns as input and store them into the variables n and m respectively. Calculate rank r of the Matrix. RankM nullityM y.

Other Math questions and answers. Of columnsn - rankr Consider the examples. Get more help from Chegg.

Finding Rank and Nullity of Matrix in C 1. Theorem 2 If a matrix A is in row echelon form then the nonzero rows of A are linearly independent. Now for part 2 assume that rankA r.

To find P such that PA A product of all elementary matrices we can append the identity matrix Im to A to form an extended matrix and row reduce the extended matrix to upper triangular form. Find the rank and nullity of the matrix. D Nullity A A 4 20 31 6 -5 -6 2 -11 -16 -.

Then r ℓ n. Theorem 385 If A is m n then rankAnullityA n. You can input only integer numbers decimals or fractions in this online calculator -24 57.

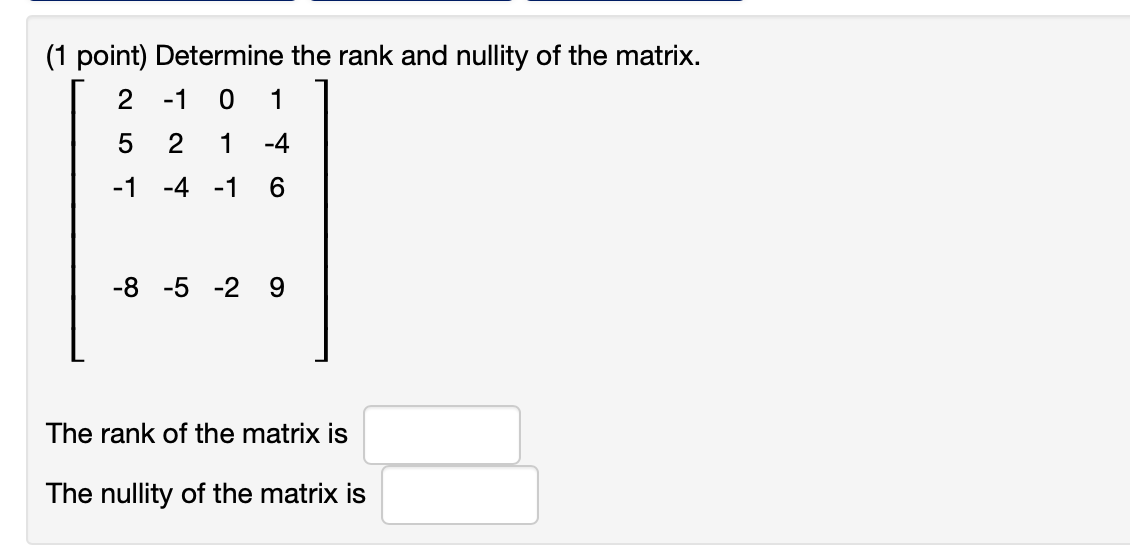
Solved 1 Point Determine The Rank And Nullity Of The Chegg Com

Compute Rank And Nullity Youtube

Solved 1 Point Find The Rank And The Nullity Of The Matrix Chegg Com

Solved Find The Rank And Nullity Of The Matrix A By Reducing Chegg Com